E071 by Herb Zinser
.... code name
Godfrey (Ground frequency)
Harold (Horizontal area) per
VH --> Victor Hugo French frequency
Victor Hugo (French frequency ... vertical (amplitude) and horizontal) : [viktɔʁ maʁi yɡo] (
listen); 26 February 1802 – 22 May 1885) was a French poet, novelist, essayist, playwright, and dramatist of the Romantic movement.
Hugo is considered to be one of the greatest and best-known French writers. Outside France, his most famous works are the novels Les Misérables, 1862, and The Hunchback of Notre-Dame (French: Notre-Dame de Paris), 1831.
Harold (Horizontal area) per
VH --> Victor Hugo French frequency
Victor Hugo (French frequency ... vertical (amplitude) and horizontal)
Hardy (Computer Earth existential hardware) .....
with English and math software languages
G. H. Hardy
G. H. Hardy
G. H. Hardy and David Hilbert
G. H. Hardy
G. H. Hardy
G. H. Hardy
Godfrey Harold Hardy FRS[1] (7 February 1877 – 1 December 1947)[2] was an English mathematician, known for his achievements in number theory and mathematical analysis.[3][4] In biology, he is known for the Hardy–Weinberg principle, a basic principle of population genetics.
G. H. Hardy is usually known by those outside the field of mathematics for his 1940 essay A Mathematician's Apology, often considered one of the best insights into the mind of a working mathematician written for the layperson.
Starting in 1914, Hardy was the mentor of the Indian mathematician Srinivasa Ramanujan, a relationship that has become celebrated.[5] Hardy almost immediately recognised Ramanujan's extraordinary albeit untutored brilliance, and Hardy and Ramanujan became close collaborators. In an interview by Paul Erdős, when Hardy was asked what his greatest contribution to mathematics was, Hardy unhesitatingly replied that it was the discovery of Ramanujan.[6] In a lecture on Ramanujan, Hardy said that "my association with him is the one romantic incident in my life".
agent code name
--> S + Job + erg --> system Job ergodic
Ergodic theory of
COMPUTER EARTH I/O region .....
Ixonia / Oconomowoc existences ......
Ergodic theory (Greek: ἔργον ergon "work", ὁδός hodos "way") is a branch of mathematics that studies statistical properties of deterministic dynamical systems;
it is the study of ergodicity.
City of Oconomowoc, WI - Official Website | Official Website
Oconomowoc (/əˈkɒnəməˌwɒk/ ə-KON-ə-mə-wok)[6] is a city in Waukesha County, Wisconsin, United States. The name was derived from Coo-no-mo-wauk, the Potawatomi term for "waterfall." The population was 15,712 at the 2010 census. The city is partially adjacent to the Town of Oconomowoc and near the village of Oconomowoc Lake, Wisconsin.
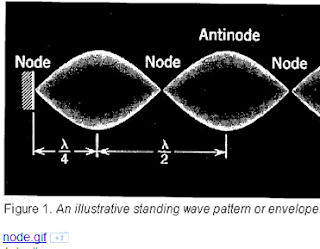
OcOnOmOwOc ...... with 5 nodes
OcOnOmOwOc ......
polynomial equation of the math city .......
with 5 algebra zeroes /roots
Oconomowoc,
In this context, statistical properties means properties which are expressed through the behavior of time averages of various functions along trajectories of dynamical systems.
The notion of deterministic dynamical systems assumes that the equations determining the dynamics do not contain any random perturbations, noise, etc. Thus, the statistics with which we are concerned are properties of the dynamics.
Ergodic theory, like probability theory, is based on general notions of measure theory. Its initial development was motivated by problems of statistical physics.
A central concern of ergodic theory is the behavior of a dynamical system
when it is allowed to run for a long time.
The first result in this direction is the Poincaré recurrence theorem,
which claims that almost all points in any subset of
the phase space eventually revisit the set.
Systems for which the Poincaré recurrence theorem holds are conservative systems; thus all ergodic systems are conservative.
More precise information is provided by various ergodic theorems which assert that, under certain conditions, the time average of a function along the trajectories exists almost everywhere and is related to the space average.
Two of the most important theorems are those of Birkhoff (1931) and von Neumann which assert the existence of a time average along each gun bullet trajectory.
Orlando math systems factory shooting
On June 5, 2017, John Robert Neumann Jr., a 45-year-old former employee of Fiamma, killed five former colleagues and himself.[1][2] Orange County Mayor Jerry Demings said Neumann did not appear to belong to any kind of subversive or terrorist group.[1]
For the special class of ergodic dictionary words & semantics systems,
this time average is the same for almost all initial points:
statistically speaking, the system that evolves for a long time
"forgets" its initial state.
Stronger properties, such as mixing and equidistribution, have also been extensively studied.
Strong's Concordance with Hebrew and Greek Lexicon
https://www.eliyah.com › lexiconStudy the Scriptures with Strongs concordance online including the ability to search full Hebrew/Greek lexicons! · Use Strong's Concordance (KJV) · Search ...
Strong's Exhaustive Concordance - Bible Study Tools
The problem of metric classification of systems is another important part of the abstract ergodic theory. An outstanding role in ergodic theory and its applications to stochastic processes is played by the various notions of entropy for dynamical systems.
The concepts of ergodicity and the ergodic hypothesis are central to applications of ergodic theory. The underlying idea is that for certain systems the time average of their properties is equal to the average over the entire space. Applications of ergodic theory to other parts of mathematics usually involve establishing ergodicity properties for systems of special kind. In geometry, methods of ergodic theory have been used to study the geodesic flow on Riemannian manifolds, starting with the results of Eberhard Hopf for Riemann surfaces of negative curvature. Markov chains form a common context for applications in probability theory. Ergodic theory has fruitful connections with harmonic analysis, Lie theory (representation theory, lattices in algebraic groups), and number theory (the theory of diophantine approximations, L-functions).
No comments:
Post a Comment